Fréchet differentiability in R2.
The concept of Fréchet (aka bounded) differentiability plays a role in our recent paper on the sensitivity of variational Bayes approximations for in discrete Bayesian nonparametrics. Fréchet differentiability is a degree of smoothness which is stronger than having a directional derivative in every direction, but weaker than being continuously differentiable.
When I was first exposed to it, Fréchet differentiability seemed like a mysterious and abstract concept, so I would like to share this following example in \(\mathbb{R}^2\) to be a useful way to motivate the concept, and to form some intuition about what Fréchet differentiability means and doesn’t mean. As far as I can recall this example is one I made up, though it is littler more than a simplified version of the more complicated (but more interesting) Example 1.9 in Averbukh and Smolyanov’s 1967 paper, “The theory of differentiation in linear topological spaces”.
What is Fréchet differentiability?
Here’s a definition of Fréchet differentiability, taken from Zeidler’s wonderful book, “Nonlinear Functional Analysis and Its Applications I: Fixed point theorems:”
Let \(B_1\) and \(B_2\) denote Banach spaces, and let \(\mathscr{B}_1 \subseteq B_1\) define an open neighborhood of \(\phi_0 \in B_1\).
A function \(f: \mathscr{B}_1 \mapsto B_2\) is Fréchet differentiable (also known as boundedly differentiable) at \(\phi_0\) if there exists a bounded linear operator, \(f^{\mathrm{lin}}: B_1 \mapsto B_2\), such that, for \(\Delta \in B_1\),
\[f(\phi_0 + \Delta) - f(\phi_0) - f_{\phi_0}^{\mathrm{lin}}(\Delta) = o(\| \Delta \|) \quad \textrm{ as }\| \Delta \| \rightarrow 0.\]Observe that the directional derivative in the direction \(\Delta\) is simply given by
\[\lim_{t \rightarrow 0} \frac{f(\phi_0 + t \Delta) - f(\phi_0)) }{t}.\]When a function is Fréchet differentiable, the directional derivative and the linear operator \(f_{\phi_0}^{\mathrm{lin}}(\Delta)\) coincide. So another way to express Fréchet differentiability is that
\[\begin{align*} % \lim_{t \rightarrow 0} \sup_{\Delta: \| \Delta \| = 1} \left| \frac{f(\phi_0 + t \Delta) - f(\phi_0) }{t} - f_{\phi_0}^{\mathrm{lin}}(\Delta) \right|\rightarrow 0. % \end{align*} %\]In other words, Fréchet differentiability implies that the directional derivative provides a uniformly good approximation in a sufficiently small ball.
An example of non-Fréchet differentiability
Most of the differentiable functions on \(\mathbb{R}^D\) that you work with in introductory math courses are Fréchet differentiable, but in functional analysis, Fréchet differentiability becomes something you cannot so readily take for granted. However, there are examples even in \(\mathbb{R}^2\) of functions that are directionally but not Fréchet differentiable, and the following is one.
Consider \((x_1, x_2) \in \mathbb{R}^2\), and the polar coordinates \(r := \sqrt{x_1^2 + x_2^2}\) and \(\theta := \arctan(x_2 / x_1)\). Let \(\{\pi k: k \in \mathbb{Z} \}\) denote integer multiples of \(\pi\). Define
\[\begin{align*} % f(r, \theta) := \begin{cases} \left(\frac{r}{| \sin \theta |}\right)^2 & \textrm{when } \theta \notin \{\pi k: k \in \mathbb{Z}\} \textrm{ and } r > 0 \\ 0 & \textrm{when } \theta \in \{\pi k: k \in \mathbb{Z} \} \textrm{ or }r = 0. % \end{cases} \end{align*}\]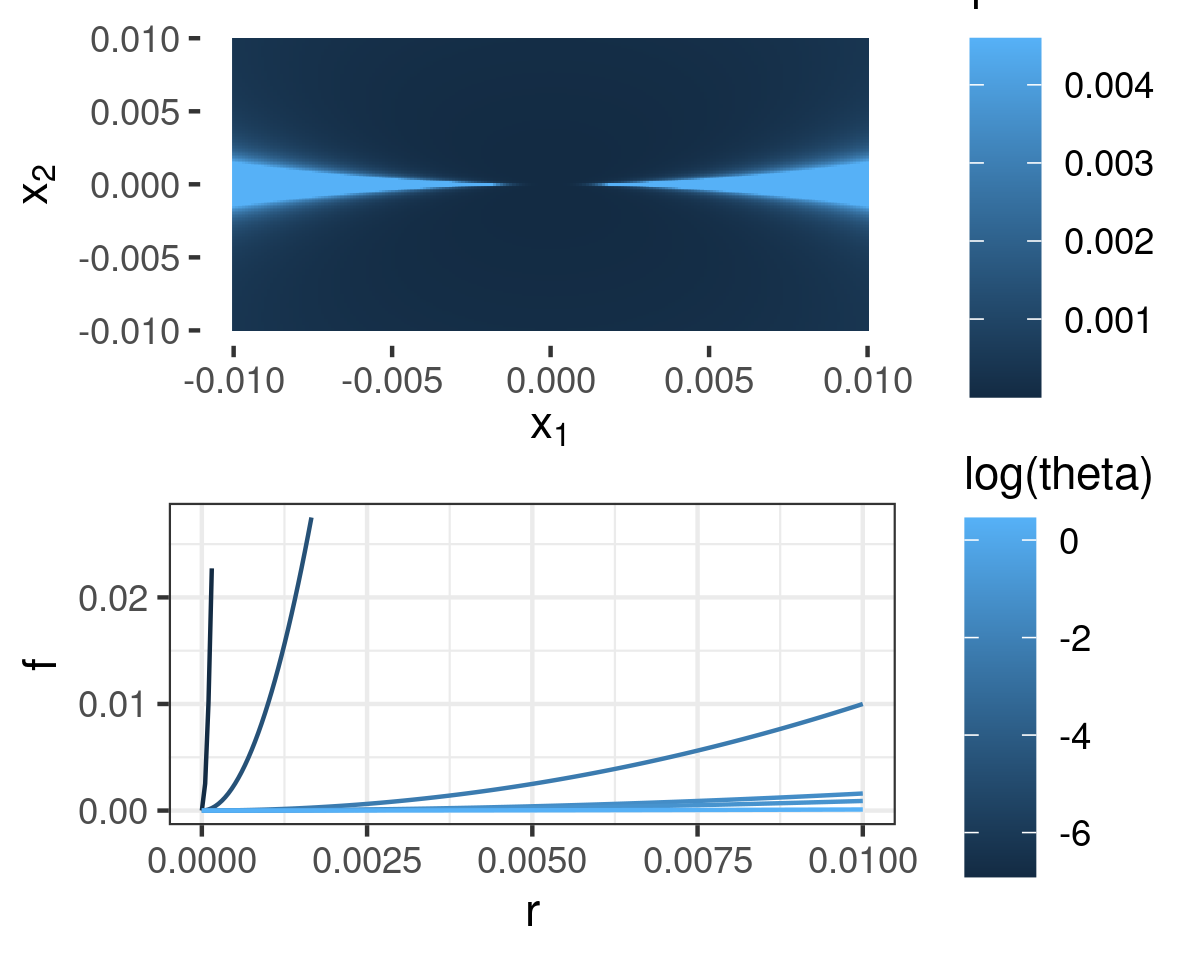
The above figure contains a plot of \(f(r, \theta)\), both over \(\mathbb{R}^2\) and along paths for particular choices of \(\theta\).
We can show that the function \(f\) has a directional derivative in every direction, but is not Fréchet differentiable. By ordinary calculus, for any \(\theta\), \(\frac{\partial f(r, \theta)}{\partial r} = 0\) at \(r=0\), so the directional derivatives all exist and are identically \(0\). However, for any \(r\), there exists a \(\theta(r)\) such that \(r / |\sin(\theta(r))| = 1\). For such a choice of \(\theta(r)\), the error in the linear approximation is \(f(r, \theta(r)) - 0 = 1/2\), which does not go to zero as \(r \rightarrow 0\).
An example of vacuous Fréchet differentiability
We can “fix” the above example by truncating the second derivative, providing a function that is Fréchet differentiable, and yet still arbitrarily badly behaved. This example serves to remind us that Fréchet differentiabilty is a fundamentally local concept—it does not guarantee the ability to meaningfully extrapolate.
In the above example, the second derivative in a particular direction is given by \(\frac{\partial^2 f(r, \theta)}{\partial r^2}|_{r=0} = \frac{1}{2 |\sin \theta|}\), which can be made arbitrarily large by taking \(\theta\) close to \(0\) or to \(\pi\). We could modify \(f(r, \theta)\) to be Fr{'e}chet differentiable by smoothly “capping” \(1 / |\sin \theta|\) at some arbitrarily large value. However, the ability to meaningfully extrapolate \(f(r, \theta)\) in the direction of a very large but finite second derivative remains limited.
In the context of the above example, fix some \(0 < M < \infty\), and define
\[% \begin{align*} % \tilde{f}(r, \theta) := \begin{cases} f(r, \theta) & \textrm{when }\frac{1}{| \sin(\theta)|} \le M \\ 0. & \textrm{when }\frac{1}{|\sin(\theta)|} > M. % \end{cases} % \end{align*} %\]Then \(\tilde{f}\) is continuous and Fréchet differentiable at \(r=0\). In this case, for any \(r\), \(\sup_{\theta} r / |\sin(\theta(r))| = r / M\), so both \(\lim_{r \rightarrow 0} \tilde{f}(r, \theta) \le \lim_{r \rightarrow 0} r^2 / M^2 = 0\) and \(\lim_{r \rightarrow 0} \tilde{f}(r, \theta) / r \le \lim_{r \rightarrow 0} r / M^2 = 0\). (Note that \(\tilde{f}\) is continuous only at \(r=0\), not on a ball centered at \(0\).)
Despite being Fréchet differentiable, the linear approximation may not extrapolate well to any finite \(r\). In the direction \(\theta = \sin^{-1}(1 / M)\), the error of the linear extrapolation to any \(r_0\) is still \(\tilde{f}(r, \theta) - 0 = M r_0^2\). Since Fréchet differentiability requires only \(M < \infty\), the extraplation error can be arbitrarily large, even for Fréchet differentiable functions.
Fréchet differentiability and extrapolation
The above examples motivate our statement in the BNP paper that Fréchet differentiability is neither necessary nor sufficient if you are interested in using derivatives to extrapolate. A function may behave quite well in a particular direction and yet fail to be Fréchet differentiable; it may be Fréchet differentiable and yet fail to extrapolate meaningfully to over a particular finite interval. (Of course, Fréchet (or at least Hadamard) differentiability is a desirable technical property, in that it suffices for nice computational tools like the chain rule, but that is a somewhat separate discussion if you can compute the needed directional derivatives directly.)